Edge contraction

Classes
class	Gudhi::contraction::Cost_policy< EdgeProfile >
	Policy to specify the cost of contracting an edge. More...
class	Gudhi::contraction::Link_condition_valid_contraction< EdgeProfile >
	Policy that only accept edges verifying the link condition (and therefore whose contraction preserving homotopy type). More...
class	Gudhi::contraction::Placement_policy< EdgeProfile >
	Policy to specify where the merged point had to be placed after an edge contraction. More...
class	Gudhi::contraction::Valid_contraction_policy< EdgeProfile >
	Policy to specify if an edge contraction is valid or not. More...
class	Gudhi::contraction::Contraction_visitor< EdgeProfile >
	Interface for a visitor of the edge contraction process. More...
class	Gudhi::contraction::Skeleton_blocker_contractor< GeometricSimplifiableComplex, EdgeProfile >
	Class that allows to contract iteratively edges of a simplicial complex. More...

Detailed Description

Author

David Salinas

Introduction

The purpose of this package is to offer a user-friendly interface for edge contraction simplification of huge simplicial complexes. It uses the Skeleton-Blocker data-structure whose size remains small during simplification
of most used geometrical complexes of topological data analysis such as the Rips or the Delaunay complexes. In practice, the size of this data-structure is even much lower than the total number of simplices.

The edge contraction operation consists in identifying two vertices of a simplicial complex. A lot of algorithms have been developed in computer graphics that allows to reduce efficiently the size of 2-dimensional simplicial complexes while preserving its geometry (for instance see [32] [39]). These approaches can be extended to higher-dimensional simplicial complexes. The main advantage of using the Skeleton-Blocker data structure for edge contraction is that when the number of blockers is small, the operations needed for edge contraction algorithms have polynomial complexity regarding the size the graph. Therefore, the simplification can be done without enumerating the set of simplices that is often non tracktable in high-dimension and is then very efficient (sub-linear with regards to the number of simplices in practice).

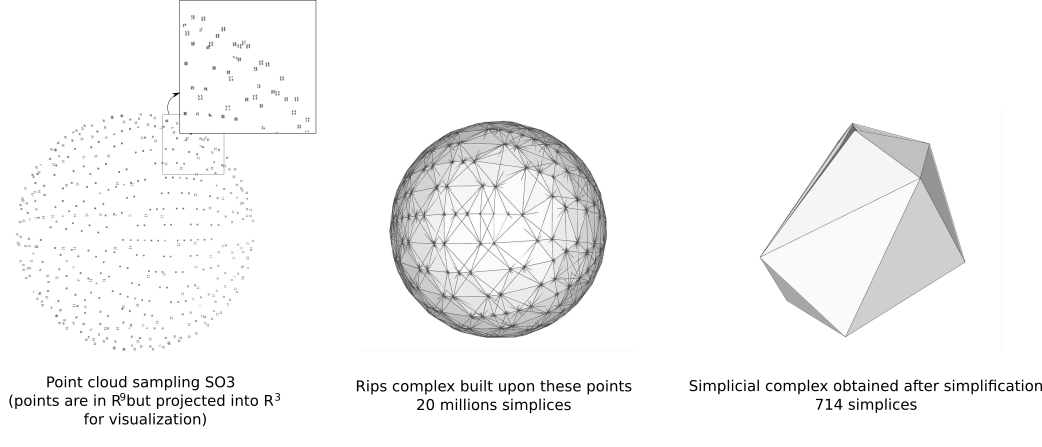
A typical application of this package is homology group computation. It is illustrated in the next figure where a Rips complex is built upon a set of high-dimensional points and simplified with edge contractions. It has initially a big number of simplices (around 20 millions) but simplifying it to a much reduced form with only 15 vertices (and 714 simplices) takes only few seconds on a desktop machine (see the example below). One can then compute homology group with a simplicial complex having very few simplices instead of running the homology algorithm on the much bigger initial set of simplices which would take much more time and memory.

Edge contraction illustration

Design

This class design is policy based and heavily inspired from the similar edge collapse package of CGAL http://doc.cgal.org/latest/Surface_mesh_simplification/index.html (which is however restricted to 2D triangulations).

Policies

Four policies can be customized in this package:

• Cost_policy: specify how much cost an edge contraction of a given edge. The edge with lowest cost is iteratively picked and contracted if valid.
• Valid_contraction_policy: specify if a given edge contraction is valid. For instance, this policy can check the link condition which ensures that the homotopy type is preserved after the edge contraction.
• Placement_policy: every time an edge is contracted, its points are merge to one point specified by this policy. This may be the middle of the edge of some more sophisticated point such as the minimum of a cost as in [32].

Visitor

A visitor which implements the class Contraction_visitor gets called at several key moments during the simplification:

• when the algorithms starts or ends,
• when an edge is seen for the first time,
• when an edge is considered for an edge contraction,
• before and after an edge is contracted.

This allows to implements most of edge contraction based algorithm with this package without having to change the main simplification source code.

Performance

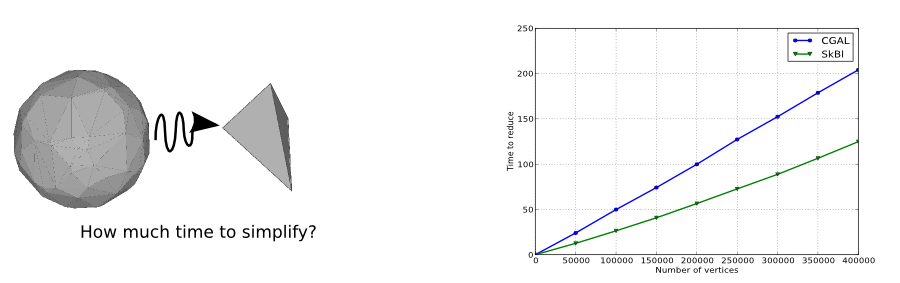
The next figure shows the computation time to reduce a random 2-sphere to a single tetrahedron with this package and with the CGAL equivalent package. Despite this package is able to deal with arbitrary simplicial complexes (any dimensions, manifold or non manifold), it is still 65% times faster than the CGAL package which is focused on 2-manifold. The main reason is that few blockers appears during the simplification and hence, the algorithm only have to deal with the graph and not higher-dimensional simplices (in this case triangles). However, we recall that higher-dimensional simplices are implicitly stored in the Skeleton-Blocker data-structure. Hence, one has to store simplices in an external map if some information needs to be associated with them (information that could be a filtration value or an orientation for instance).

Time in seconds to simplify random 2-spheres to a tetrahedron

Example

This example loads points from an OFF file and builds the Rips complex with an user provided parameter. It then simplifies the built Rips complex while ensuring its homotopy type is preserved during the contraction (edge are contracted only when the link condition is valid).

#include <boost/timer/timer.hpp>
#include <iostream>
#include <gudhi/Edge_contraction.h>
#include <gudhi/Skeleton_blocker.h>
#include <gudhi/Off_reader.h>
 
 
using namespace std;
using namespace Gudhi;
using namespace skeleton_blocker;
using namespace contraction;
 
struct Geometry_trait{
  typedef std::vector<double> Point;
};
 
typedef Geometry_trait::Point Point;
typedef Skeleton_blocker_simple_geometric_traits<Geometry_trait> Complex_geometric_traits;
typedef Skeleton_blocker_geometric_complex< Complex_geometric_traits > Complex;
typedef Edge_profile<Complex> Profile;
typedef Skeleton_blocker_contractor<Complex> Complex_contractor;
 
template<typename Point>
double eucl_distance(const Point& a,const Point& b){
  double res = 0;
  auto a_coord = a.begin();
  auto b_coord = b.begin();
  for(; a_coord != a.end(); a_coord++, b_coord++){
    res += (*a_coord - *b_coord) * (*a_coord - *b_coord);
  }
  return sqrt(res);
}
 
template<typename ComplexType>
void build_rips(ComplexType& complex, double offset){
  if (offset<=0) return;
  auto vertices = complex.vertex_range();
  for (auto p = vertices.begin(); p != vertices.end(); ++p)
    for (auto q = p; ++q != vertices.end(); )
      if (eucl_distance(complex.point(*p), complex.point(*q)) < 2 * offset)
        complex.add_edge_without_blockers(*p,*q);
}
 
int main (int argc, char *argv[])
{
  if (argc!=3){
    std::cerr << "Usage "<<argv[0]<<" ../../data/points/tore3D_1307.off 0.3 to load the file ../../data/points/tore3D_1307.off and contract the Rips complex built with parameter 0.3.\n";
    return -1;
  }
 
  Complex complex;
 
  // load the points
  Skeleton_blocker_off_reader<Complex> off_reader(argv[1],complex,true);
  if(!off_reader.is_valid()){
    std::cerr << "Unable to read file:"<<argv[1]<<std::endl;
    return EXIT_FAILURE;
  }
  std::clog << "Build the Rips complex"<<std::endl;
 
  build_rips(complex,atof(argv[2]));
 
  boost::timer::auto_cpu_timer t;
 
  std::clog << "Initial complex has "<<
      complex.num_vertices()<<" vertices and "<<
      complex.num_edges()<<" edges"<<std::endl;
 
  Complex_contractor contractor(complex,
      new Edge_length_cost<Profile>,
      contraction::make_first_vertex_placement<Profile>(),
      contraction::make_link_valid_contraction<Profile>(),
      contraction::make_remove_popable_blockers_visitor<Profile>());
  contractor.contract_edges();
 
  std::clog << "Counting final number of simplices \n";
  unsigned num_simplices = std::distance(complex.star_simplex_range().begin(),complex.star_simplex_range().end());
 
  std::clog << "Final complex has "<<
      complex.num_vertices()<<" vertices, "<<
      complex.num_edges()<<" edges, "<<
      complex.num_blockers()<<" blockers and "<<
      num_simplices<<" simplices"<<std::endl;
 
 
  std::clog << "Time to simplify and enumerate simplices:\n";
 
  return EXIT_SUCCESS;
}

./example/Contraction/RipsContraction /path/to/gudhi-data/points/SO3/SO3_10000.off 0.3
[ 50%] [100%] Built target SkeletonBlockerIteration
Built target RipsContraction
Build the Rips complex
Initial complex has 10000 vertices and 195664 edges
Counting final number of simplices 
Final complex has 15 vertices, 101 edges, 165 blockers and 714 simplices
Time to simplify and enumerate simplices:
 3.166621s wall, 3.150000s user + 0.010000s system = 3.160000s CPU (99.8%)

The SO3 dataset used here can be found in gudhi-data repository.