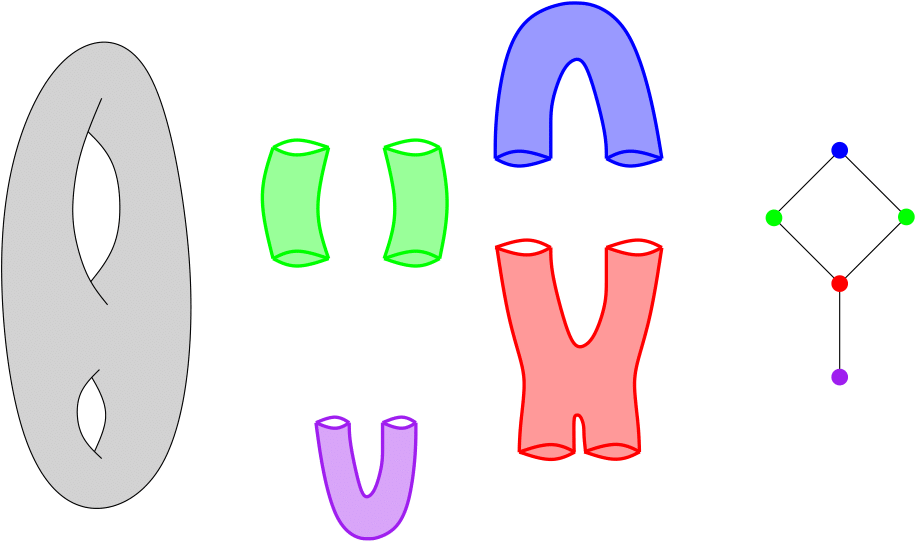Cover complex

Classes
class	Gudhi::cover_complex::Cover_complex< Point >
	Cover complex data structure. More...

Detailed Description

Author

Mathieu Carrière

Visualizations of the simplicial complexes can be done with either neato (from graphviz), geomview, KeplerMapper. Input point clouds are assumed to be OFF files

Covers

Nerves and Graph Induced Complexes require a cover C of the input point cloud P, that is a set of subsets of P whose union is P itself. Very often, this cover is obtained from the preimage of a family of intervals covering the image of some scalar-valued function f defined on P. This family is parameterized by its resolution, which can be either the number or the length of the intervals, and its gain, which is the overlap percentage between consecutive intervals (ordered by their first values).

Nerves

Nerve definition

Assume you are given a cover C of your point cloud P. Then, the Nerve of this cover is the simplicial complex that has one k-simplex per k-fold intersection of cover elements. See also Wikipedia .

Nerve of a double torus

Example

This example builds the Nerve of a point cloud sampled on a 3D human shape (human.off). The cover C comes from the preimages of intervals (10 intervals with gain 0.3) covering the height function (coordinate 2), which are then refined into their connected components using the triangulation of the .OFF file.

/*    This file is part of the Gudhi Library - https://gudhi.inria.fr/ - which is released under MIT.
 *    See file LICENSE or go to https://gudhi.inria.fr/licensing/ for full license details.
 *    Author(s):       Mathieu Carrière
 *
 *    Copyright (C) 2017 Inria
 *
 *    Modification(s):
 *      - YYYY/MM Author: Description of the modification
 */
 
#include <gudhi/GIC.h>
 
#include <string>
#include <vector>
 
void usage(int nbArgs, char *const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off coordinate resolution gain [-v] \n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/human.off 2 10 0.3 -v \n";
  exit(-1);  // ----- >>
}
 
int main(int argc, char **argv) {
  if ((argc != 5) && (argc != 6)) usage(argc, argv[0]);
 
  using Point = std::vector<float>;
 
  std::string off_file_name(argv[1]);
  int coord = atoi(argv[2]);
  int resolution = atoi(argv[3]);
  double gain = atof(argv[4]);
  bool verb = 0;
  if (argc == 6) verb = 1;
 
  // --------------------------------
  // Init of a Nerve from an OFF file
  // --------------------------------
 
  Gudhi::cover_complex::Cover_complex<Point> SC;
  SC.set_verbose(verb);
 
  bool check = SC.read_point_cloud(off_file_name);
 
  if (!check) {
    std::clog << "Incorrect OFF file." << std::endl;
  } else {
    SC.set_type("Nerve");
 
    SC.set_color_from_coordinate(coord);
    SC.set_function_from_coordinate(coord);
 
    SC.set_graph_from_OFF();
    SC.set_resolution_with_interval_number(resolution);
    SC.set_gain(gain);
    SC.set_cover_from_function();
 
    SC.find_simplices();
 
    SC.write_info();
 
    Gudhi::Simplex_tree<> stree;
    SC.create_complex(stree);
    SC.compute_PD();
 
    // ----------------------------------------------------------------------------
    // Display information about the graph induced complex
    // ----------------------------------------------------------------------------
 
    if (verb) {
      std::clog << "Nerve is of dimension " << stree.dimension() << " - " << stree.num_simplices() << " simplices - "
                << stree.num_vertices() << " vertices." << std::endl;
 
      std::clog << "Iterator on Nerve simplices" << std::endl;
      for (auto f_simplex : stree.filtration_simplex_range()) {
        for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
          std::clog << vertex << " ";
        }
        std::clog << std::endl;
      }
    }
  }
 
  return 0;
}

When launching:

$> ./Nerve ../../data/points/human.off 2 10 0.3 -v

the program output is:

Min function value = -0.979672 and Max function value = 0.816414
Interval 0 = [-0.979672, -0.761576]
Interval 1 = [-0.838551, -0.581967]
Interval 2 = [-0.658942, -0.402359]
Interval 3 = [-0.479334, -0.22275]
Interval 4 = [-0.299725, -0.0431415]
Interval 5 = [-0.120117, 0.136467]
Interval 6 = [0.059492, 0.316076]
Interval 7 = [0.239101, 0.495684]
Interval 8 = [0.418709, 0.675293]
Interval 9 = [0.598318, 0.816414]
Computing preimages...
Computing connected components...
.txt generated. It can be visualized with e.g. python KeplerMapperVisuFromTxtFile.py and firefox.
5 interval(s) in dimension 0:
  [-0.909111, 0.00817529]
  [-0.171433, 0.367392]
  [-0.171433, 0.367392]
  [-0.909111, 0.745853]
0 interval(s) in dimension 1:
Nerve is of dimension 1 - 41 simplices - 21 vertices.
Iterator on Nerve simplices
1 
0 
4 
4 0 
2 
2 1 
8 
8 2 
5 
5 4 
9 
9 8 
13 
13 5 
14 
14 9 
19 
19 13 
25 
32 
20 
32 20 
33 
33 25 
26 
26 14 
26 19 
42 
42 26 
34 
34 33 
27 
27 20 
35 
35 27 
35 34 
42 35 
44 
44 35 
54 
54 44 

The program also writes a file ../../data/points/human_sc.txt. The first three lines in this file are the location of the input point cloud and the function used to compute the cover. The fourth line contains the number of vertices nv and edges ne of the Nerve. The next nv lines represent the vertices. Each line contains the vertex ID, the number of data points it contains, and their average color function value. Finally, the next ne lines represent the edges, characterized by the ID of their vertices.

Using KeplerMapper, one can obtain the following visualization:

Visualization with KeplerMapper

Graph Induced Complexes (GIC)

GIC definition

Again, assume you are given a cover C of your point cloud P. Moreover, assume you are also given a graph G built on top of P. Then, for any clique in G whose nodes all belong to different elements of C, the GIC includes a corresponding simplex, whose dimension is the number of nodes in the clique minus one. See [25] for more details.

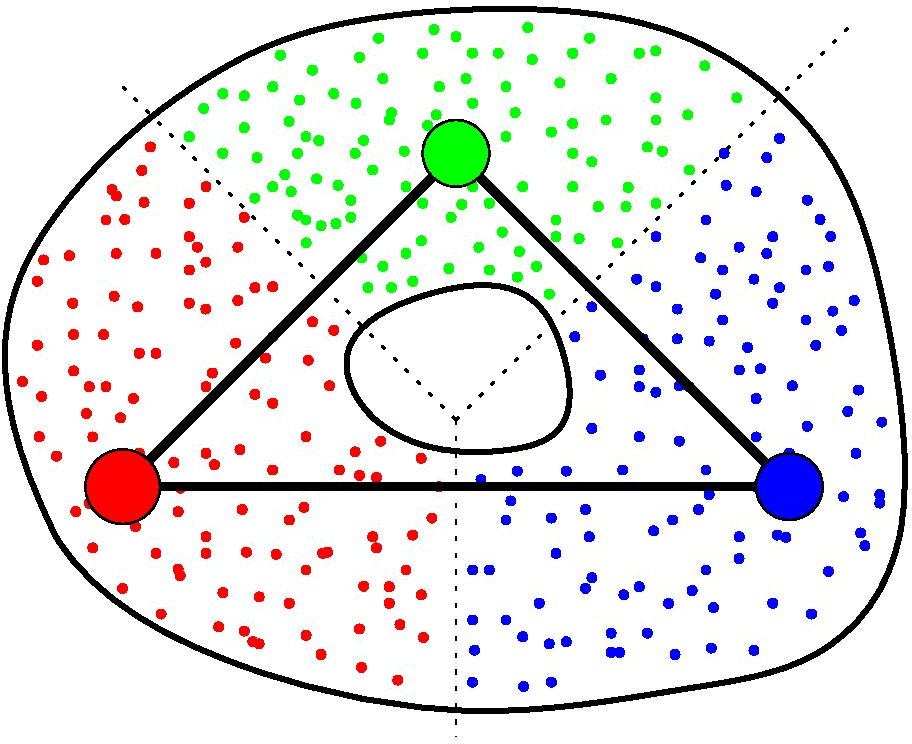
GIC of a point cloud.

Example with cover from Voronoï

This example builds the GIC of a point cloud sampled on a 3D human shape (human.off). We randomly subsampled 100 points in the point cloud, which act as seeds of a geodesic Voronoï diagram. Each cell of the diagram is then an element of C. The graph G (used to compute both the geodesics for Voronoï and the GIC) comes from the triangulation of the human shape. Note that the resulting simplicial complex is in dimension 3 in this example.

/*    This file is part of the Gudhi Library - https://gudhi.inria.fr/ - which is released under MIT.
 *    See file LICENSE or go to https://gudhi.inria.fr/licensing/ for full license details.
 *    Author(s):       Mathieu Carrière
 *
 *    Copyright (C) 2017 Inria
 *
 *    Modification(s):
 *      - YYYY/MM Author: Description of the modification
 */
 
#include <gudhi/GIC.h>
 
#include <string>
#include <vector>
 
void usage(int nbArgs, char *const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off N [-v] \n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/human.off 100 -v \n";
  exit(-1);  // ----- >>
}
 
int main(int argc, char **argv) {
  if ((argc != 3) && (argc != 4)) usage(argc, argv[0]);
 
  using Point = std::vector<float>;
 
  std::string off_file_name(argv[1]);
  int m = atoi(argv[2]);
  bool verb = 0;
  if (argc == 4) verb = 1;
 
  // ----------------------------------------------------------------------------
  // Init of a graph induced complex from an OFF file
  // ----------------------------------------------------------------------------
 
  Gudhi::cover_complex::Cover_complex<Point> GIC;
  GIC.set_verbose(verb);
 
  bool check = GIC.read_point_cloud(off_file_name);
 
  if (!check) {
    std::clog << "Incorrect OFF file." << std::endl;
  } else {
    GIC.set_type("GIC");
 
    GIC.set_color_from_coordinate();
 
    GIC.set_graph_from_OFF();
    GIC.set_cover_from_Voronoi(Gudhi::Euclidean_distance(), m);
 
    GIC.find_simplices();
 
    GIC.plot_OFF();
 
    Gudhi::Simplex_tree<> stree;
    GIC.create_complex(stree);
 
    // ----------------------------------------------------------------------------
    // Display information about the graph induced complex
    // ----------------------------------------------------------------------------
 
    if (verb) {
      std::clog << "Graph induced complex is of dimension " << stree.dimension() << " - " << stree.num_simplices()
                << " simplices - " << stree.num_vertices() << " vertices." << std::endl;
 
      std::clog << "Iterator on graph induced complex simplices" << std::endl;
      for (auto f_simplex : stree.filtration_simplex_range()) {
        for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
          std::clog << vertex << " ";
        }
        std::clog << std::endl;
      }
    }
  }
 
  return 0;
}

When launching:

$> ./VoronoiGIC ../../data/points/human.off 700 -v

the program outputs SC.off. Using e.g.

$> geomview ../../data/points/human_sc.off

one can obtain the following visualization:

Visualization with Geomview

Functional GIC

If one restricts to the cliques in G whose nodes all belong to preimages of consecutive intervals (assuming the cover of the height function is minimal, i.e. no more than two intervals can intersect at a time), the GIC is of dimension one, i.e. a graph. We call this graph the functional GIC. See [14] for more details.

Example

Functional GIC comes with automatic selection of the Rips threshold, the resolution and the gain of the function cover. See [17] for more details. In this example, we compute the functional GIC of a Klein bottle embedded in R^5, where the graph G comes from a Rips complex with automatic threshold, and the cover C comes from the preimages of intervals covering the first coordinate, with automatic resolution and gain. Note that automatic threshold, resolution and gain can be computed as well for the Nerve.

/*    This file is part of the Gudhi Library - https://gudhi.inria.fr/ - which is released under MIT.
 *    See file LICENSE or go to https://gudhi.inria.fr/licensing/ for full license details.
 *    Author(s):       Mathieu Carrière
 *
 *    Copyright (C) 2017 Inria
 *
 *    Modification(s):
 *      - YYYY/MM Author: Description of the modification
 */
 
#include <gudhi/GIC.h>
 
#include <string>
#include <vector>
 
void usage(int nbArgs, char *const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off coordinate [-v] \n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/human.off 2 -v \n";
  exit(-1);  // ----- >>
}
 
int main(int argc, char **argv) {
  if ((argc != 3) && (argc != 4)) usage(argc, argv[0]);
 
  using Point = std::vector<float>;
 
  std::string off_file_name(argv[1]);
  int coord = atoi(argv[2]);
  bool verb = 0;
  if (argc == 4) verb = 1;
 
  // -----------------------------------------
  // Init of a functional GIC from an OFF file
  // -----------------------------------------
 
  Gudhi::cover_complex::Cover_complex<Point> GIC;
  GIC.set_verbose(verb);
 
  bool check = GIC.read_point_cloud(off_file_name);
 
  if (!check) {
    std::clog << "Incorrect OFF file." << std::endl;
  } else {
    GIC.set_type("GIC");
 
    GIC.set_color_from_coordinate(coord);
    GIC.set_function_from_coordinate(coord);
 
    GIC.set_graph_from_automatic_rips(Gudhi::Euclidean_distance());
    GIC.set_automatic_resolution();
    GIC.set_gain();
    GIC.set_cover_from_function();
 
    GIC.find_simplices();
 
    GIC.compute_distribution(10);
    GIC.compute_p_value();
 
    GIC.plot_DOT();
 
    Gudhi::Simplex_tree<> stree;
    GIC.create_complex(stree);
 
    // --------------------------------------------
    // Display information about the functional GIC
    // --------------------------------------------
 
    if (verb) {
      std::clog << "Coordinate GIC is of dimension " << stree.dimension() << " - " << stree.num_simplices()
                << " simplices - " << stree.num_vertices() << " vertices." << std::endl;
 
      std::clog << "Iterator on coordinate GIC simplices" << std::endl;
      for (auto f_simplex : stree.filtration_simplex_range()) {
        for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
          std::clog << vertex << " ";
        }
        std::clog << std::endl;
      }
    }
  }
 
  return 0;
}

When launching:

$> ./CoordGIC ../../data/points/KleinBottle5D.off 0 -v

the program outputs SC.dot. Using e.g.

$> neato SC.dot -Tpdf -o SC.pdf

one can obtain the following visualization:

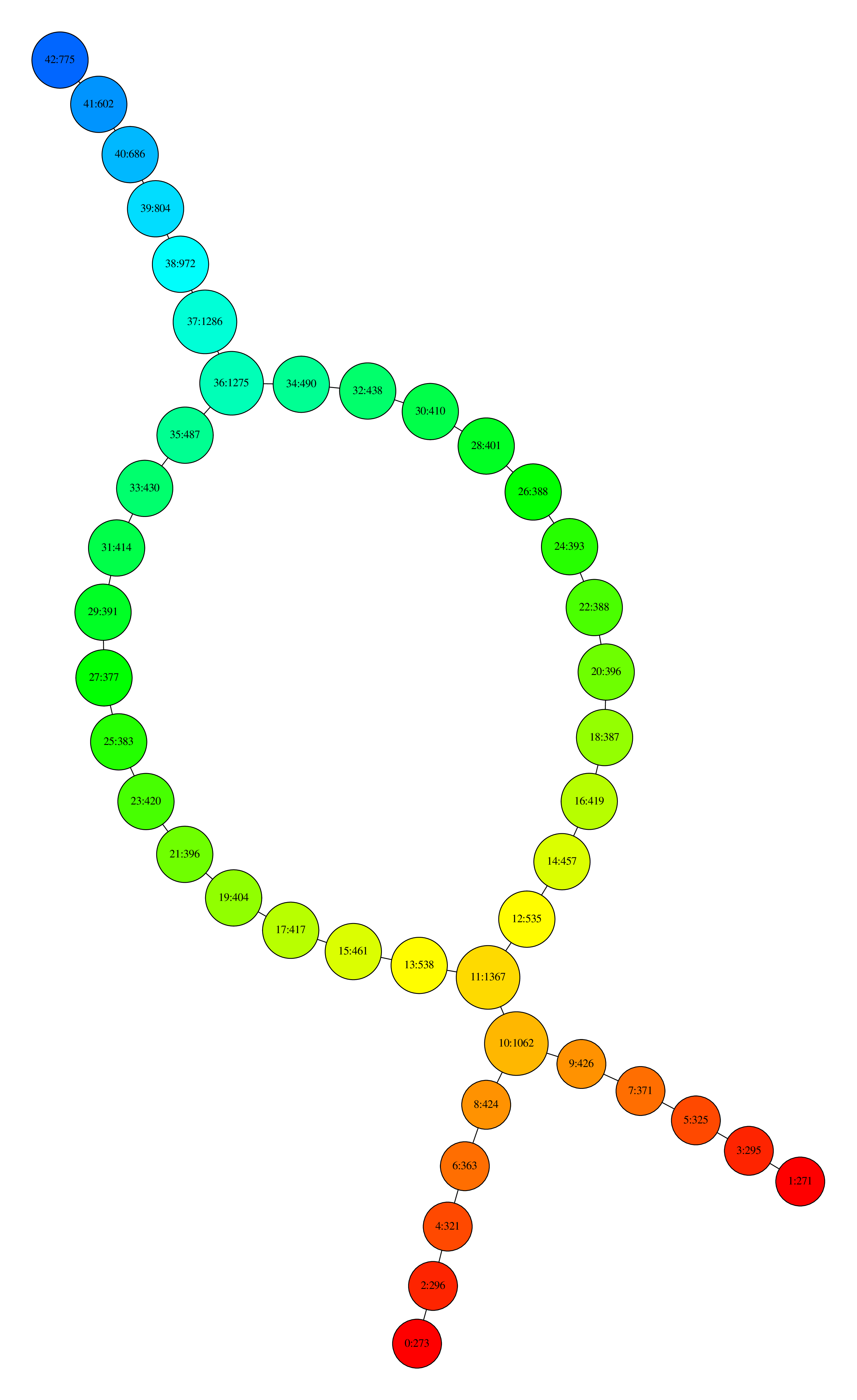
Visualization with Neato

where nodes are colored by the filter function values and, for each node, the first number is its ID and the second is the number of data points that its contain.

We also provide an example on a set of 72 pictures taken around the same object (lucky_cat.off). The function is now the first eigenfunction given by PCA, whose values are written in a file (lucky_cat_PCA1). Threshold, resolution and gain are automatically selected as before.

/*    This file is part of the Gudhi Library - https://gudhi.inria.fr/ - which is released under MIT.
 *    See file LICENSE or go to https://gudhi.inria.fr/licensing/ for full license details.
 *    Author(s):       Mathieu Carrière
 *
 *    Copyright (C) 2017 Inria
 *
 *    Modification(s):
 *      - YYYY/MM Author: Description of the modification
 */
 
#include <gudhi/GIC.h>
 
#include <string>
#include <vector>
 
void usage(int nbArgs, char *const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off function [-v] \n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/COIL_database/lucky_cat.off "
                                              "../../data/points/COIL_database/lucky_cat_PCA1 -v \n";
  exit(-1);  // ----- >>
}
 
int main(int argc, char **argv) {
  if ((argc != 3) && (argc != 4)) usage(argc, argv[0]);
 
  using Point = std::vector<float>;
 
  std::string off_file_name(argv[1]);
  std::string func_file_name = argv[2];
  bool verb = 0;
  if (argc == 4) verb = 1;
 
  // -----------------------------------------
  // Init of a functional GIC from an OFF file
  // -----------------------------------------
 
  Gudhi::cover_complex::Cover_complex<Point> GIC;
  GIC.set_verbose(verb);
 
  bool check = GIC.read_point_cloud(off_file_name);
 
  if (!check) {
    std::clog << "Incorrect OFF file." << std::endl;
  } else {
    GIC.set_type("GIC");
 
    GIC.set_color_from_file(func_file_name);
    GIC.set_function_from_file(func_file_name);
 
    GIC.set_graph_from_automatic_rips(Gudhi::Euclidean_distance());
    GIC.set_automatic_resolution();
    GIC.set_gain();
    GIC.set_cover_from_function();
 
    GIC.find_simplices();
 
    GIC.plot_DOT();
 
    Gudhi::Simplex_tree<> stree;
    GIC.create_complex(stree);
 
    // --------------------------------------------
    // Display information about the functional GIC
    // --------------------------------------------
 
    if (verb) {
      std::clog << "Functional GIC is of dimension " << stree.dimension() << " - " << stree.num_simplices()
                << " simplices - " << stree.num_vertices() << " vertices." << std::endl;
 
      std::clog << "Iterator on functional GIC simplices" << std::endl;
      for (auto f_simplex : stree.filtration_simplex_range()) {
        for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
          std::clog << vertex << " ";
        }
        std::clog << std::endl;
      }
    }
  }
 
  return 0;
}

When launching:

$> ./FuncGIC ../../data/points/COIL_database/lucky_cat.off ../../data/points/COIL_database/lucky_cat_PCA1 -v

the program outputs again SC.dot which gives the following visualization after using neato:

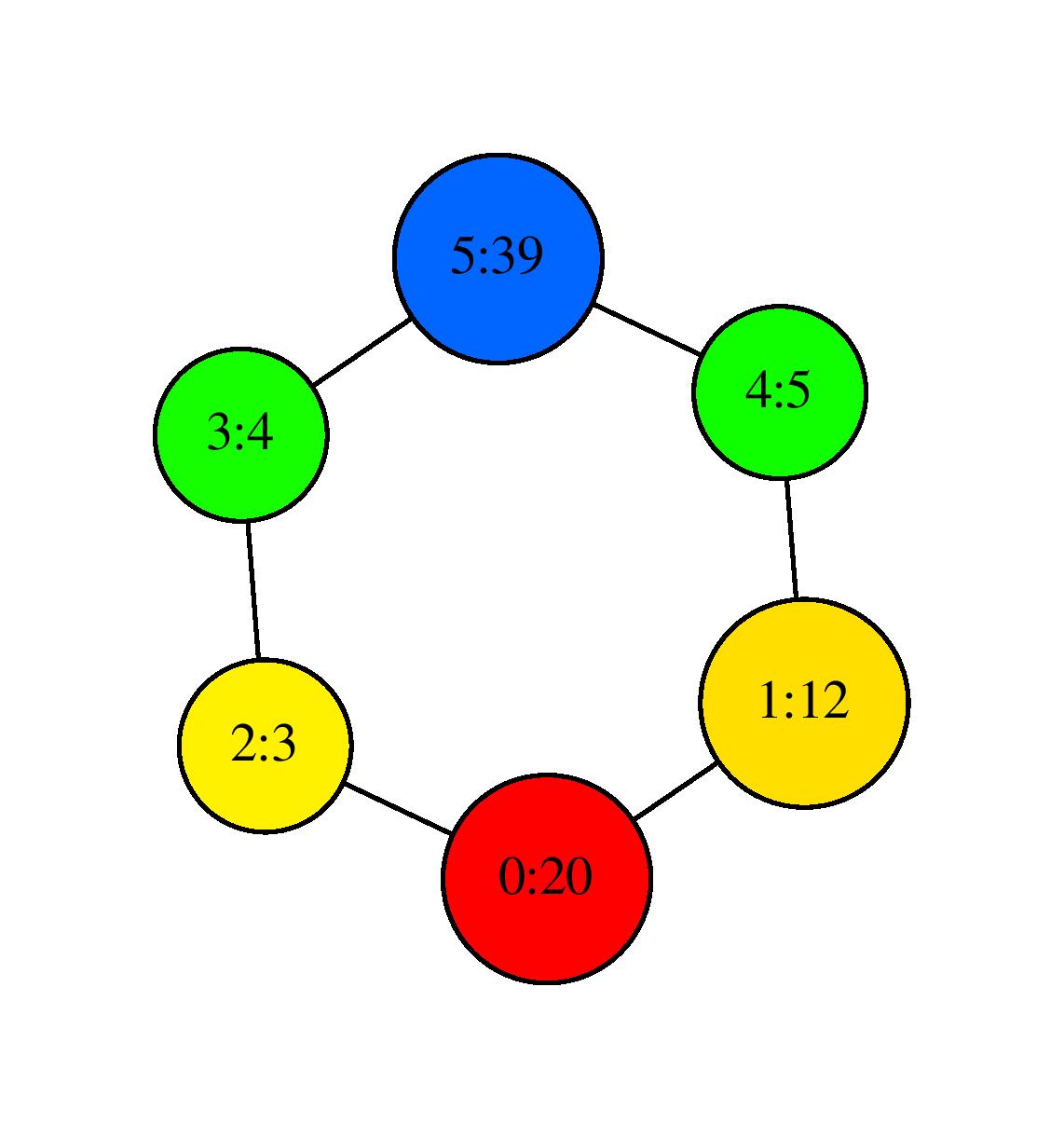
Visualization with neato