- Author
- Clément Maria, Pawel Dlotko, Vincent Rouvreau, Marc Glisse
Rips complex definition
The Vietoris-Rips complex (Wikipedia) is an abstract simplicial complex defined on a finite metric space, where each simplex corresponds to a subset of points whose diameter is smaller that some given threshold. Varying the threshold, we can also see the Rips complex as a filtration of the \((n-1)-\)dimensional simplex, where the filtration value of each simplex is the diameter of the corresponding subset of points.
This filtered complex is most often used as an approximation of the Čech complex. After rescaling (Rips using the length of the edges and Čech the half-length), they share the same 1-skeleton and are multiplicatively 2-interleaved or better. While it is slightly bigger, it is also much easier to compute.
The number of simplices in the full Rips complex is exponential in the number of vertices, it is thus usually restricted, by excluding all the simplices with filtration value larger than some threshold, and keeping only the dim_max-skeleton. It may also be a good idea to start by making the point set sparser, for instance with Gudhi::subsampling::sparsify_point_set(), since small clusters of points have a disproportionate cost without affecting the persistence diagram much.
In order to build this complex, the algorithm first builds the graph. The filtration value of each edge is computed from a user-given distance function, or directly read from the distance matrix. In a second step, this graph is inserted in a simplicial complex, which then gets expanded to a flag complex.
The input can be given as a range of points and a distance function, or as a distance matrix.
Vertex name correspond to the index of the point in the given range (aka. the point cloud).
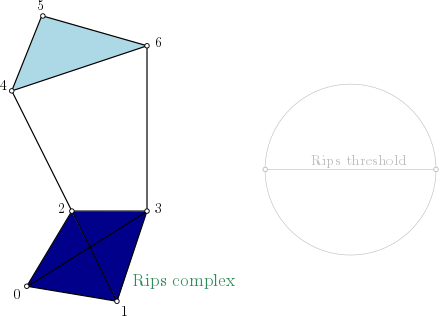
Rips-complex one skeleton graph representation
On this example, as edges (4,5), (4,6) and (5,6) are in the complex, simplex (4,5,6) is added with the filtration value set with \(max(filtration(4,5), filtration(4,6), filtration(5,6))\). And so on for simplex (0,1,2,3).
If the Rips_complex interfaces are not detailed enough for your need, please refer to the example Persistent_cohomology/rips_persistence_step_by_step.cpp , where the constructions of the graph and the Simplex_tree are more detailed.
Sparse Rips complex
Even truncated in filtration value and dimension, the Rips complex remains quite large. However, it is possible to approximate it by a much smaller filtered simplicial complex (linear size, with constants that depend on ε and the doubling dimension of the space) that is \((1+O(\epsilon))-\)interleaved with it (in particular, their persistence diagrams are at log-bottleneck distance at most \(O(\epsilon)\)).
The sparse Rips filtration was introduced by Don Sheehy [43]. We are using the version described in [12] (except that we multiply all filtration values by 2, to match the usual Rips complex), for which [18] proves a \((1,\frac{1}{1-\epsilon})\)-interleaving, although in practice the error is usually smaller. A more intuitive presentation of the idea is available in [18], and in a video [19].
The interface of Sparse_rips_complex is similar to the one for the usual Rips_complex, except that one has to specify the approximation factor. There is an option to limit the minimum and maximum filtration values, but they are not recommended: the way the approximation is done means that larger filtration values are much cheaper to handle than low filtration values, so the gain in ignoring the large ones is small, and Gudhi::subsampling::sparsify_point_set() is a more efficient way of ignoring small filtration values.
Theoretical guarantees are only available for \(\epsilon<1\). The construction accepts larger values of ε, and the size of the complex keeps decreasing, but there is no guarantee on the quality of the result. Note that while the number of edges decreases when ε increases, the number of higher-dimensional simplices may not be monotonous when \(\frac12\leq\epsilon\leq 1\).
Point cloud and distance function
Example from a point cloud and a distance function
This example builds the one skeleton graph from the given points, threshold value, and distance function. Then it creates a Simplex_tree with it.
Then, it is asked to display information about the simplicial complex.
#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <iostream>
#include <string>
#include <vector>
#include <limits>
int main() {
using Point = std::vector<double>;
std::vector<Point> points;
points.push_back({1.0, 1.0});
points.push_back({7.0, 0.0});
points.push_back({4.0, 6.0});
points.push_back({9.0, 6.0});
points.push_back({0.0, 14.0});
points.push_back({2.0, 19.0});
points.push_back({9.0, 17.0});
double threshold = 12.0;
rips_complex_from_points.create_complex(stree, 1);
std::clog << "Rips complex is of dimension " << stree.dimension() <<
std::clog << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
std::endl;
std::clog << " ( ";
std::clog << vertex << " ";
}
std::clog <<
") -> " <<
"[" << stree.
filtration(f_simplex) <<
"] ";
std::clog << std::endl;
}
return 0;
}
Compute the Euclidean distance between two Points given by a range of coordinates....
Definition: distance_functions.h:32
Options::Filtration_value Filtration_value
Type for the value of the filtration function.
Definition: Simplex_tree.h:102
Filtration_simplex_range const & filtration_simplex_range(Indexing_tag=Indexing_tag())
Returns a range over the simplices of the simplicial complex, in the order of the filtration.
Definition: Simplex_tree.h:338
Simplex_vertex_range simplex_vertex_range(Simplex_handle sh) const
Returns a range over the vertices of a simplex.
Definition: Simplex_tree.h:349
static Filtration_value filtration(Simplex_handle sh)
Returns the filtration value of a simplex.
Definition: Simplex_tree.h:614
size_t num_vertices() const
Returns the number of vertices in the complex.
Definition: Simplex_tree.h:651
size_t num_simplices()
Returns the number of simplices in the simplex_tree.
Definition: Simplex_tree.h:664
Rips complex data structure.
Definition: Rips_complex.h:45
Global distance functions.
Value type for a filtration function on a cell complex.
Definition: FiltrationValue.h:20
When launching (Rips maximal distance between 2 points is 12.0, is expanded until dimension 1 - one skeleton graph in other words):
$> ./Rips_complex_example_one_skeleton_from_points
the program output is:
Rips complex is of dimension 1 - 18 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
( 0 ) -> [0]
( 1 ) -> [0]
( 2 ) -> [0]
( 3 ) -> [0]
( 4 ) -> [0]
( 5 ) -> [0]
( 6 ) -> [0]
( 3 2 ) -> [5]
( 5 4 ) -> [5.38516]
( 2 0 ) -> [5.83095]
( 1 0 ) -> [6.08276]
( 3 1 ) -> [6.32456]
( 2 1 ) -> [6.7082]
( 6 5 ) -> [7.28011]
( 4 2 ) -> [8.94427]
( 3 0 ) -> [9.43398]
( 6 4 ) -> [9.48683]
( 6 3 ) -> [11]
Example from OFF file
This example builds the Rips_complex from the given points in an OFF file, threshold value, and distance function. Then it creates a Simplex_tree with it.
Then, it is asked to display information about the Rips complex.
#include <gudhi/Rips_complex.h>
#include <gudhi/Points_off_io.h>
#include <gudhi/Simplex_tree.h>
#include <iostream>
#include <string>
#include <vector>
void usage(int nbArgs, char * const progName) {
std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
std::cerr << "Usage: " << progName << " filename.off threshold dim_max [ouput_file.txt]\n";
std::cerr << " i.e.: " << progName << " ../../data/points/alphacomplexdoc.off 60.0\n";
exit(-1);
}
int main(int argc, char **argv) {
if ((argc != 4) && (argc != 5)) usage(argc, (argv[0] - 1));
std::string off_file_name(argv[1]);
double threshold = atof(argv[2]);
int dim_max = atoi(argv[3]);
using Point = std::vector<float>;
std::streambuf* streambuffer;
std::ofstream ouput_file_stream;
if (argc == 5) {
ouput_file_stream.open(std::string(argv[4]));
streambuffer = ouput_file_stream.rdbuf();
} else {
streambuffer = std::clog.rdbuf();
}
rips_complex_from_file.create_complex(stree, dim_max);
std::ostream output_stream(streambuffer);
output_stream << "Rips complex is of dimension " << stree.dimension() <<
output_stream << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
std::endl;
output_stream << " ( ";
output_stream << vertex << " ";
}
output_stream <<
") -> " <<
"[" << stree.
filtration(f_simplex) <<
"] ";
output_stream << std::endl;
}
ouput_file_stream.close();
return 0;
}
OFF file reader implementation in order to read points from an OFF file.
Definition: Points_off_io.h:122
When launching:
$> ./Rips_complex_example_from_off ../../data/points/alphacomplexdoc.off 12.0 3
the program output is:
Rips complex is of dimension 3 - 24 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
( 0 ) -> [0]
( 1 ) -> [0]
( 2 ) -> [0]
( 3 ) -> [0]
( 4 ) -> [0]
( 5 ) -> [0]
( 6 ) -> [0]
( 3 2 ) -> [5]
( 5 4 ) -> [5.38516]
( 2 0 ) -> [5.83095]
( 1 0 ) -> [6.08276]
( 3 1 ) -> [6.32456]
( 2 1 ) -> [6.7082]
( 2 1 0 ) -> [6.7082]
( 3 2 1 ) -> [6.7082]
( 6 5 ) -> [7.28011]
( 4 2 ) -> [8.94427]
( 3 0 ) -> [9.43398]
( 3 1 0 ) -> [9.43398]
( 3 2 0 ) -> [9.43398]
( 3 2 1 0 ) -> [9.43398]
( 6 4 ) -> [9.48683]
( 6 5 4 ) -> [9.48683]
( 6 3 ) -> [11]
Example of a sparse Rips from a point cloud
This example builds the full sparse Rips of a set of 2D Euclidean points, then prints some minimal information about the complex.
#include <gudhi/Sparse_rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <iostream>
#include <vector>
int main() {
using Point = std::vector<double>;
Point points[] = {{1.0, 1.0}, {7.0, 0.0}, {4.0, 6.0}, {9.0, 6.0}, {0.0, 14.0}, {2.0, 19.0}, {9.0, 17.0}};
double epsilon = 2;
sparse_rips.create_complex(stree, 10);
std::clog <<
"Sparse Rips complex is of dimension " << stree.dimension() <<
" - " << stree.
num_simplices()
<<
" simplices - " << stree.
num_vertices() <<
" vertices." << std::endl;
}
Sparse Rips complex data structure.
Definition: Sparse_rips_complex.h:104
When launching:
$> ./Rips_complex_example_sparse
the program output may be (the exact output varies from one run to the next):
Sparse Rips complex is of dimension 2 - 19 simplices - 7 vertices.
Distance matrix
Example from a distance matrix
This example builds the one skeleton graph from the given distance matrix and threshold value. Then it creates a Simplex_tree with it.
Then, it is asked to display information about the simplicial complex.
#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <iostream>
#include <string>
#include <vector>
#include <limits>
int main() {
using Distance_matrix = std::vector<std::vector<Filtration_value>>;
Distance_matrix distances;
distances.push_back({});
distances.push_back({0.94});
distances.push_back({0.77, 0.26});
distances.push_back({0.99, 0.99, 0.28});
distances.push_back({0.11, 0.39, 0.97, 0.30});
double threshold = 1.0;
Rips_complex rips_complex_from_points(distances, threshold);
rips_complex_from_points.create_complex(stree, 1);
std::clog << "Rips complex is of dimension " << stree.dimension() <<
std::clog << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
std::endl;
std::clog << " ( ";
std::clog << vertex << " ";
}
std::clog <<
") -> " <<
"[" << stree.
filtration(f_simplex) <<
"] ";
std::clog << std::endl;
}
return 0;
}
When launching (Rips maximal distance between 2 points is 1.0, is expanded until dimension 1 - one skeleton graph with other words):
$> ./Rips_complex_example_one_skeleton_from_distance_matrix
the program output is:
Rips complex is of dimension 1 - 18 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
( 0 ) -> [0]
( 1 ) -> [0]
( 2 ) -> [0]
( 3 ) -> [0]
( 4 ) -> [0]
( 5 ) -> [0]
( 6 ) -> [0]
( 3 2 ) -> [5]
( 5 4 ) -> [5.38516]
( 2 0 ) -> [5.83095]
( 1 0 ) -> [6.08276]
( 3 1 ) -> [6.32456]
( 2 1 ) -> [6.7082]
( 6 5 ) -> [7.28011]
( 4 2 ) -> [8.94427]
( 3 0 ) -> [9.43398]
( 6 4 ) -> [9.48683]
( 6 3 ) -> [11]
Example from a distance matrix read in a csv file
This example builds the one skeleton graph from the given distance matrix read in a csv file and threshold value. Then it creates a Simplex_tree with it.
Then, it is asked to display information about the Rips complex.
#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <iostream>
#include <string>
#include <vector>
void usage(int nbArgs, char * const progName) {
std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
std::cerr << "Usage: " << progName << " filename.csv threshold dim_max [ouput_file.txt]\n";
std::cerr << " i.e.: " << progName << " ../../data/distance_matrix/full_square_distance_matrix.csv 1.0 3\n";
exit(-1);
}
int main(int argc, char **argv) {
if ((argc != 4) && (argc != 5)) usage(argc, (argv[0] - 1));
std::string csv_file_name(argv[1]);
double threshold = atof(argv[2]);
int dim_max = atoi(argv[3]);
using Distance_matrix = std::vector<std::vector<Filtration_value>>;
Distance_matrix distances = Gudhi::read_lower_triangular_matrix_from_csv_file<Filtration_value>(csv_file_name);
std::streambuf* streambuffer;
std::ofstream ouput_file_stream;
if (argc == 5) {
ouput_file_stream.open(std::string(argv[4]));
streambuffer = ouput_file_stream.rdbuf();
} else {
streambuffer = std::clog.rdbuf();
}
rips_complex_from_file.create_complex(stree, dim_max);
std::ostream output_stream(streambuffer);
output_stream << "Rips complex is of dimension " << stree.dimension() <<
output_stream << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
std::endl;
output_stream << " ( ";
output_stream << vertex << " ";
}
output_stream <<
") -> " <<
"[" << stree.
filtration(f_simplex) <<
"] ";
output_stream << std::endl;
}
ouput_file_stream.close();
return 0;
}
This file includes common file reader for GUDHI.
When launching:
$> ./Rips_complex_example_from_csv_distance_matrix ../../data/distance_matrix/full_square_distance_matrix.csv 1.0 3
the program output is:
Rips complex is of dimension 3 - 24 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
( 0 ) -> [0]
( 1 ) -> [0]
( 2 ) -> [0]
( 3 ) -> [0]
( 4 ) -> [0]
( 5 ) -> [0]
( 6 ) -> [0]
( 3 2 ) -> [5]
( 5 4 ) -> [5.38516]
( 2 0 ) -> [5.83095]
( 1 0 ) -> [6.08276]
( 3 1 ) -> [6.32456]
( 2 1 ) -> [6.7082]
( 2 1 0 ) -> [6.7082]
( 3 2 1 ) -> [6.7082]
( 6 5 ) -> [7.28011]
( 4 2 ) -> [8.94427]
( 3 0 ) -> [9.43398]
( 3 1 0 ) -> [9.43398]
( 3 2 0 ) -> [9.43398]
( 3 2 1 0 ) -> [9.43398]
( 6 4 ) -> [9.48683]
( 6 5 4 ) -> [9.48683]
( 6 3 ) -> [11]
Correlation matrix
Analogously to the case of distance matrix, Rips complexes can be also constructed based on correlation matrix. Given a correlation matrix M, comportment-wise 1-M is a distance matrix. This example builds the one skeleton graph from the given corelation matrix and threshold value. Then it creates a Simplex_tree with it.
Then, it is asked to display information about the simplicial complex.
#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <iostream>
#include <string>
#include <vector>
#include <limits>
int main() {
using Distance_matrix = std::vector<std::vector<Filtration_value>>;
Distance_matrix correlations;
correlations.push_back({});
correlations.push_back({0.06});
correlations.push_back({0.23, 0.74});
correlations.push_back({0.01, 0.01, 0.72});
correlations.push_back({0.89, 0.61, 0.03, 0.7});
double threshold = 0;
for (size_t i = 0; i != correlations.size(); ++i) {
for (size_t j = 0; j != correlations[i].size(); ++j) {
if ((correlations[i][j] < -1) || (correlations[i][j] > 1)) {
std::cerr << "The input matrix is not a correlation matrix. The program will now terminate.\n";
throw "The input matrix is not a correlation matrix. The program will now terminate.\n";
}
correlations[i][j] = 1 - correlations[i][j];
if (correlations[i][j] > threshold) threshold = correlations[i][j];
}
}
Distance_matrix distances = correlations;
Rips_complex rips_complex_from_points(distances, threshold);
rips_complex_from_points.create_complex(stree, 1);
std::clog <<
"Rips complex is of dimension " << stree.dimension() <<
" - " << stree.
num_simplices() <<
" simplices - "
std::clog << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" << std::endl;
std::clog << " ( ";
std::clog << vertex << " ";
}
std::clog << ") -> "
std::clog << std::endl;
}
return 0;
}
When launching:
$> ./example_one_skeleton_from_correlation_matrix
the program output is:
Rips complex is of dimension 1 - 15 simplices - 5 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
( 0 ) -> [0]
( 1 ) -> [0]
( 2 ) -> [0]
( 3 ) -> [0]
( 4 ) -> [0]
( 4 0 ) -> [0.11]
( 2 1 ) -> [0.26]
( 3 2 ) -> [0.28]
( 4 3 ) -> [0.3]
( 4 1 ) -> [0.39]
( 2 0 ) -> [0.77]
( 1 0 ) -> [0.94]
( 4 2 ) -> [0.97]
( 3 0 ) -> [0.99]
( 3 1 ) -> [0.99]
All the other constructions discussed for Rips complex for distance matrix can be also performed for Rips complexes construction from correlation matrices.
- Warning
- As persistence diagrams points will be under the diagonal, bottleneck distance and persistence graphical tool will not work properly, this is a known issue.
