Simplex tree user manual#
Definition#
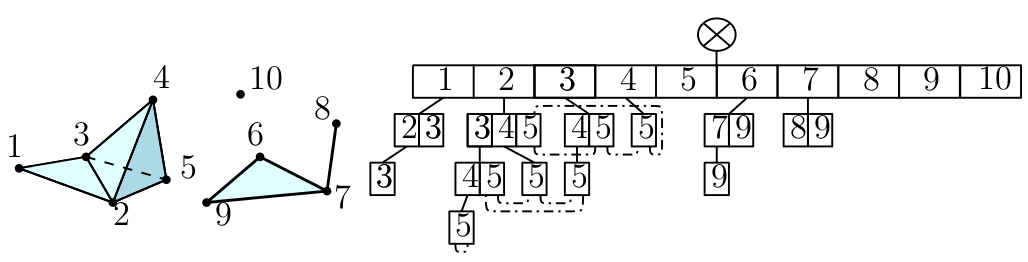
|
The simplex tree is an efficient and flexible data structure for representing general (filtered) simplicial complexes. The data structure is described in [5] |
|

|
||
A simplicial complex \(\mathbf{K}\) on a set of vertices \(V = \{1, \cdots ,|V|\}\) is a collection of simplices \(\{\sigma\}\), \(\sigma \subseteq V\) such that \(\tau \subseteq \sigma \in \mathbf{K} \rightarrow \tau \in \mathbf{K}\). The dimension \(n=|\sigma|-1\) of \(\sigma\) is its number of elements minus 1.
A filtration of a simplicial complex is a function \(f:\mathbf{K} \rightarrow \mathbb{R}\) satisfying \(f(\tau)\leq f(\sigma)\) whenever \(\tau \subseteq \sigma\). Ordering the simplices by increasing filtration values (breaking ties so as a simplex appears after its subsimplices of same filtration value) provides an indexing scheme.
Implementation#
The simplex tree is an efficient and flexible data structure for representing general
(filtered) simplicial complexes.
The data structure is described in [5].
Example#
import gudhi
st = gudhi.SimplexTree()
if st.insert([0, 1]):
print("[0, 1] inserted")
if st.insert([0, 1, 2], filtration=4.0):
print("[0, 1, 2] inserted")
if st.find([0, 1]):
print("[0, 1] found")
result_str = 'num_vertices=' + repr(st.num_vertices())
print(result_str)
result_str = 'num_simplices=' + repr(st.num_simplices())
print(result_str)
print("skeleton(2) =")
for sk_value in st.get_skeleton(2):
print(sk_value)
The output is:
[0, 1] inserted
[0, 1, 2] inserted
[0, 1] found
num_vertices=3
num_simplices=7
skeleton(2) =
([0, 1, 2], 4.0)
([0, 1], 0.0)
([0, 2], 4.0)
([0], 0.0)
([1, 2], 4.0)
([1], 0.0)
([2], 4.0)