Tangential complex user manual#
|
A Tangential Delaunay complex is a simplicial complex designed to reconstruct a \(k\)-dimensional manifold embedded in \(d\)-dimensional Euclidean space. The input is a point sample coming from an unknown manifold. The running time depends only linearly on the extrinsic dimension \(d\) and exponentially on the intrinsic dimension \(k\). |
|
Definition#
A Tangential Delaunay complex is a simplicial complex designed to reconstruct a \(k\)-dimensional smooth manifold embedded in \(d\)-dimensional Euclidean space. The input is a point sample coming from an unknown manifold, which means that the points lie close to a structure of “small” intrinsic dimension. The running time depends only linearly on the extrinsic dimension \(d\) and exponentially on the intrinsic dimension \(k\).
An extensive description of the Tangential complex can be found in [4].
What is a Tangential Complex?#
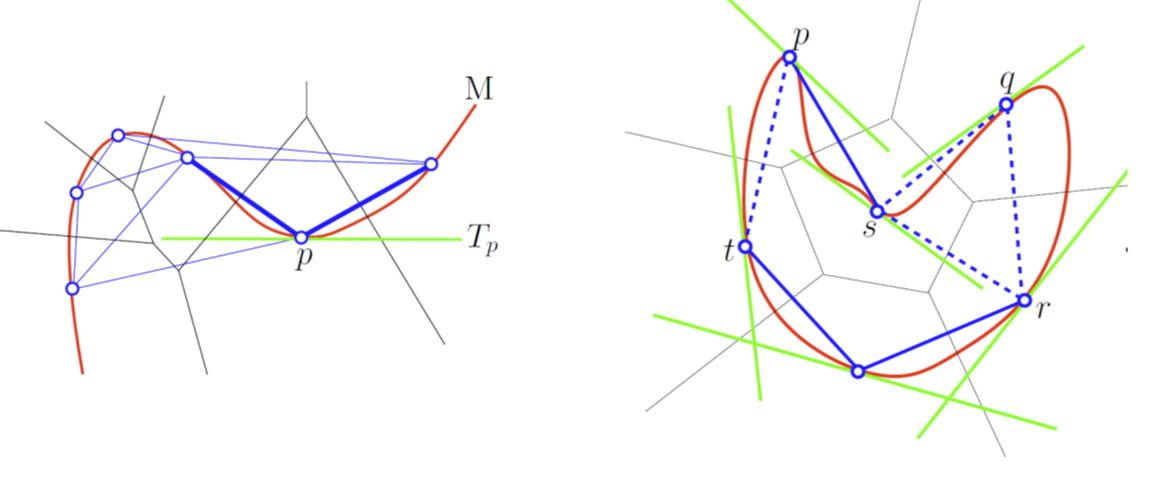
Let us start with the description of the Tangential complex of a simple example, with \(k = 1\) and \(d = 2\). The point set \(\mathscr P\) is located on a closed curve embedded in 2D. Only 4 points will be displayed (more are required for PCA) to simplify the figures.
The input#
For each point \(P\), estimate its tangent subspace \(T_P\) using PCA.
The estimated normals#
Let us add the Voronoi diagram of the points in orange. For each point \(P\), construct its star in the Delaunay triangulation of \(\mathscr P\) restricted to \(T_P\).
The Voronoi diagram#
The Tangential Delaunay complex is the union of those stars.
In practice, neither the ambient Voronoi diagram nor the ambient Delaunay triangulation is computed. Instead, local \(k\)-dimensional regular triangulations are computed with a limited number of points as we only need the star of each point. More details can be found in [4].
Inconsistencies#
Inconsistencies between the stars can occur. An inconsistency occurs when a simplex is not in the star of all its vertices.
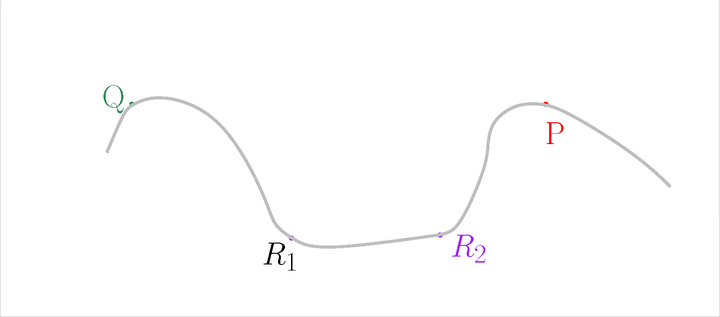
Let us take the same example.
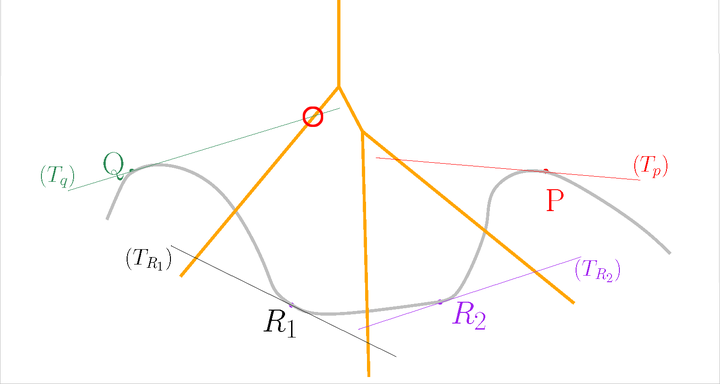
Before#
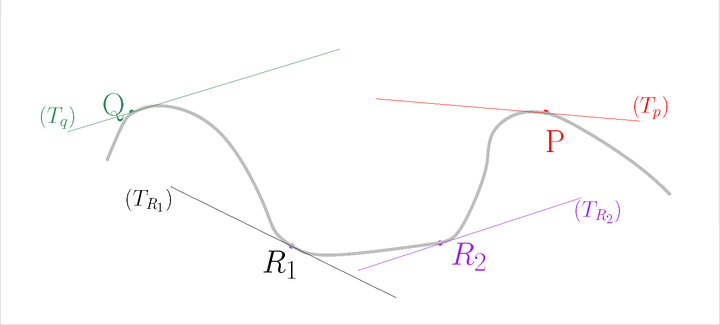
Let us slightly move the tangent subspace \(T_Q\)
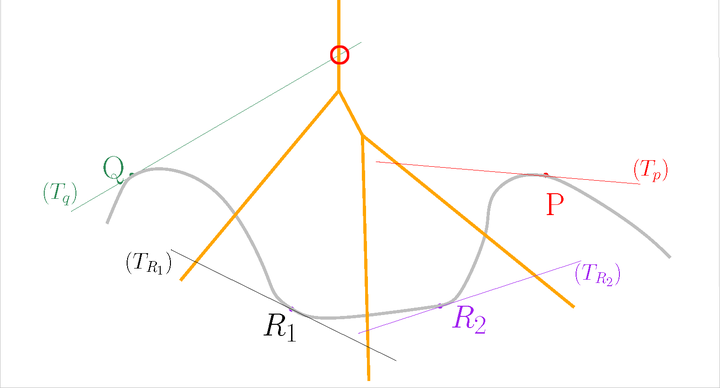
After#
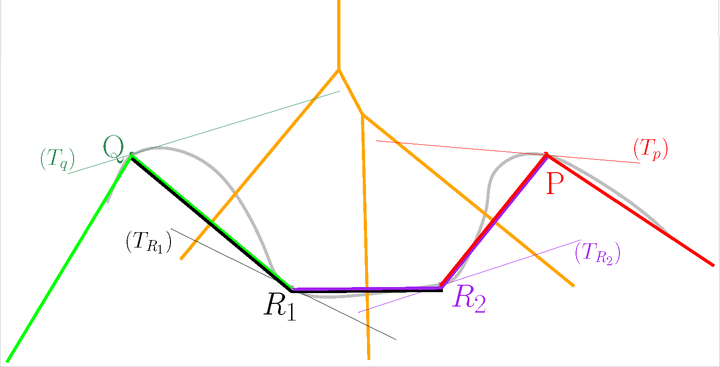
Now, the star of \(Q\) contains \(QP\), but the star of \(P\) does not contain \(QP\). We have an inconsistency.
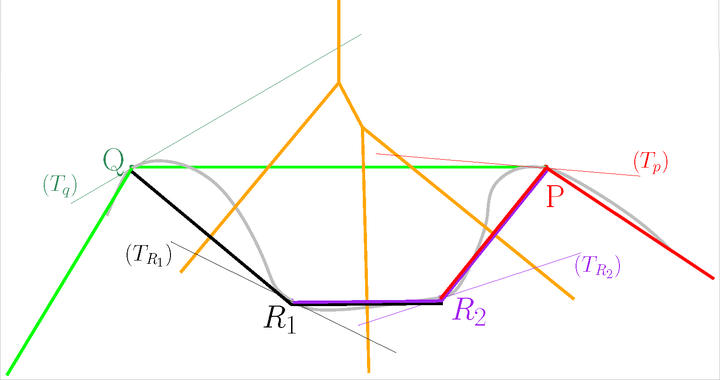
After#
One way to solve inconsistencies is to randomly perturb the positions of the points involved in an inconsistency. In the current implementation, this perturbation is done in the tangent subspace of each point. The maximum perturbation radius is given as a parameter to the constructor.
In most cases, we recommend to provide a point set where the minimum distance between any two points is not too small. This can be achieved using the functions provided by the Subsampling module. Then, a good value to start with for the maximum perturbation radius would be around half the minimum distance between any two points. The Example with perturbation below shows an example of such a process.
In most cases, this process is able to dramatically reduce the number of inconsistencies, but is not guaranteed to succeed.
Output#
The result of the computation is exported as a SimplexTree. It is the union of
the stars of all the input points. A vertex in the Simplex Tree is the index of
the point in the range provided by the user. The point corresponding to a
vertex can also be obtained through the gudhi.TangentialComplex.get_point() function.
Note that even if the positions of the points are perturbed, their original
positions are kept (e.g. get_point() returns the original
position of the point).
The result can be obtained after the computation of the Tangential complex itself and/or after the perturbation process.
Simple example#
This example builds the Tangential complex of point set read in an OFF file.
import gudhi
tc = gudhi.TangentialComplex(intrisic_dim = 1,
off_file=gudhi.__root_source_dir__ + '/data/points/alphacomplexdoc.off')
tc.compute_tangential_complex()
result_str = 'Tangential contains ' + repr(tc.num_simplices()) + \
' simplices - ' + repr(tc.num_vertices()) + ' vertices.'
print(result_str)
st = tc.create_simplex_tree()
result_str = 'Simplex tree is of dimension ' + repr(st.dimension()) + \
' - ' + repr(st.num_simplices()) + ' simplices - ' + \
repr(st.num_vertices()) + ' vertices.'
print(result_str)
for filtered_value in st.get_filtration():
print(filtered_value[0])
The output is:
Tangential contains 12 simplices - 7 vertices.
Simplex tree is of dimension 1 - 15 simplices - 7 vertices.
[0]
[1]
[0, 1]
[2]
[0, 2]
[1, 2]
[3]
[1, 3]
[4]
[2, 4]
[5]
[4, 5]
[6]
[3, 6]
[5, 6]
Example with perturbation#
This example builds the Tangential complex of a point set, then tries to solve inconsistencies by perturbing the positions of points involved in inconsistent simplices.
import gudhi
tc = gudhi.TangentialComplex(intrisic_dim = 1,
points=[[0.0, 0.0], [1.0, 0.0], [0.0, 1.0], [1.0, 1.0]])
tc.compute_tangential_complex()
result_str = 'Tangential contains ' + repr(tc.num_vertices()) + ' vertices.'
print(result_str)
if tc.num_inconsistent_simplices() > 0:
print('Tangential contains inconsistencies.')
tc.fix_inconsistencies_using_perturbation(10, 60)
if tc.num_inconsistent_simplices() == 0:
print('Inconsistencies has been fixed.')
The output is:
Tangential contains 4 vertices.
Inconsistencies has been fixed.