Witness complex user manual#
|
Witness complex \(Wit(W,L)\) is a simplicial complex defined on two sets of points in \(\mathbb{R}^D\). The data structure is described in [5]. |
|
Definitions#
Witness complex is a simplicial complex defined on two sets of points in \(\mathbb{R}^D\):
\(W\) set of witnesses and
\(L\) set of landmarks.
Even though often the set of landmarks \(L\) is a subset of the set of witnesses \(W\), it is not a requirement for the current implementation.
Landmarks are the vertices of the simplicial complex and witnesses help to decide on which simplices are inserted via a predicate “is witnessed”.
De Silva and Carlsson in their paper [14] differentiate weak witnessing and strong witnessing:
weak: \(\sigma \subset L\) is witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L \setminus \sigma},\ d(w,l) \leq d(w,l')\)
strong: \(\sigma \subset L\) is witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L},\ d(w,l) \leq d(w,l')\)
where \(d(.,.)\) is a distance function.
Both definitions can be relaxed by a real value \(\alpha\):
weak: \(\sigma \subset L\) is \(\alpha\)-witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L \setminus \sigma},\ d(w,l)^2 \leq d(w,l')^2 + \alpha^2\)
strong: \(\sigma \subset L\) is \(\alpha\)-witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L},\ d(w,l)^2 \leq d(w,l')^2 + \alpha^2\)
which leads to definitions of weak relaxed witness complex (or just relaxed witness complex for short) and strong relaxed witness complex respectively.
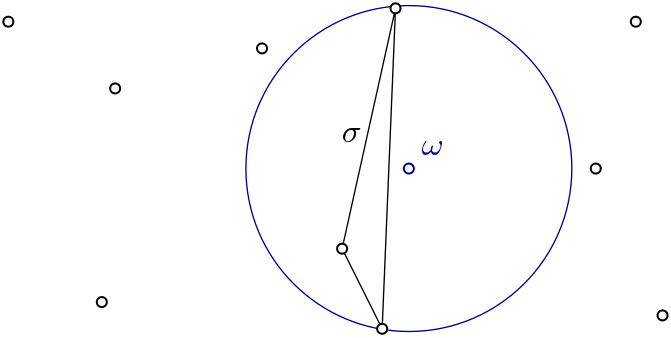
Strongly witnessed simplex#
In particular case of 0-relaxation, weak complex corresponds to witness complex introduced in
[14], whereas 0-relaxed strong witness complex consists of just vertices and is not very
interesting. Hence for small relaxation weak version is preferable.
However, to capture the homotopy type (for example using gudhi.SimplexTree.persistence()) it is
often necessary to work with higher filtration values. In this case strong relaxed witness complex is faster to compute
and offers similar results.
Implementation#
The two complexes described above are implemented in the corresponding classes
The construction of the Euclidean versions of complexes follow the same scheme:
Construct a search tree on landmarks.
Construct lists of nearest landmarks for each witness.
Construct the witness complex for nearest landmark lists.
In the non-Euclidean classes, the lists of nearest landmarks are supposed to be given as input.
The constructors take on the steps 1 and 2, while the function create_complex() executes the step 3.
Constructing weak relaxed witness complex from an off file#
Let’s start with a simple example, which reads an off point file and computes a weak witness complex.
import gudhi
import argparse
parser = argparse.ArgumentParser(description='EuclideanWitnessComplex creation from '
'points read in a OFF file.',
epilog='Example: '
'example/witness_complex_diagram_persistence_from_off_file_example.py '
'-f ../data/points/tore3D_300.off -a 1.0 -n 20 -d 2'
'- Constructs a alpha complex with the '
'points from the given OFF file.')
parser.add_argument("-f", "--file", type=str, required=True)
parser.add_argument("-a", "--max_alpha_square", type=float, required=True)
parser.add_argument("-n", "--number_of_landmarks", type=int, required=True)
parser.add_argument("-d", "--limit_dimension", type=int, required=True)
args = parser.parse_args()
with open(args.file, 'r') as f:
first_line = f.readline()
if (first_line == 'OFF\n') or (first_line == 'nOFF\n'):
print("#####################################################################")
print("EuclideanWitnessComplex creation from points read in a OFF file")
witnesses = gudhi.read_points_from_off_file(off_file=args.file)
landmarks = gudhi.pick_n_random_points(points=witnesses, nb_points=args.number_of_landmarks)
message = "EuclideanWitnessComplex with max_edge_length=" + repr(args.max_alpha_square) + \
" - Number of landmarks=" + repr(args.number_of_landmarks)
print(message)
witness_complex = gudhi.EuclideanWitnessComplex(witnesses=witnesses, landmarks=landmarks)
simplex_tree = witness_complex.create_simplex_tree(max_alpha_square=args.max_alpha_square,
limit_dimension=args.limit_dimension)
message = "Number of simplices=" + repr(simplex_tree.num_simplices())
print(message)
else:
print(args.file, "is not a valid OFF file")
f.close()
Example2: Computing persistence using strong relaxed witness complex#
Here is an example of constructing a strong witness complex filtration and computing persistence on it: