Alpha complex user manual¶
Definition¶
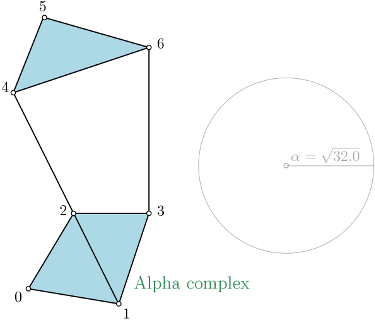
|
Alpha complex is a simplicial complex constructed from the finite cells of a Delaunay Triangulation. The filtration value of each simplex is computed as the square of the circumradius of the simplex if the circumsphere is empty (the simplex is then said to be Gabriel), and as the minimum of the filtration values of the codimension 1 cofaces that make it not Gabriel otherwise. For performances reasons, it is advised to use CGAL \(\geq\) 5.0.0. |
|
AlphaComplex is constructing a SimplexTree using Delaunay Triangulation [14] from the Computational Geometry Algorithms Library [27].
Remarks¶
When an \(\alpha\)-complex is constructed with an infinite value of \(\alpha^2\), the complex is a Delaunay complex (with special filtration values).
Example from points¶
This example builds the alpha-complex from the given points:
import gudhi
alpha_complex = gudhi.AlphaComplex(points=[[1, 1], [7, 0], [4, 6], [9, 6], [0, 14], [2, 19], [9, 17]])
simplex_tree = alpha_complex.create_simplex_tree()
result_str = 'Alpha complex is of dimension ' + repr(simplex_tree.dimension()) + ' - ' + \
repr(simplex_tree.num_simplices()) + ' simplices - ' + \
repr(simplex_tree.num_vertices()) + ' vertices.'
print(result_str)
fmt = '%s -> %.2f'
for filtered_value in simplex_tree.get_filtration():
print(fmt % tuple(filtered_value))
The output is:
Alpha complex is of dimension 2 - 25 simplices - 7 vertices.
[0] -> 0.00
[1] -> 0.00
[2] -> 0.00
[3] -> 0.00
[4] -> 0.00
[5] -> 0.00
[6] -> 0.00
[2, 3] -> 6.25
[4, 5] -> 7.25
[0, 2] -> 8.50
[0, 1] -> 9.25
[1, 3] -> 10.00
[1, 2] -> 11.25
[1, 2, 3] -> 12.50
[0, 1, 2] -> 13.00
[5, 6] -> 13.25
[2, 4] -> 20.00
[4, 6] -> 22.74
[4, 5, 6] -> 22.74
[3, 6] -> 30.25
[2, 6] -> 36.50
[2, 3, 6] -> 36.50
[2, 4, 6] -> 37.24
[0, 4] -> 59.71
[0, 2, 4] -> 59.71
Algorithm¶
Data structure¶
In order to build the alpha complex, first, a Simplex tree is built from the cells of a Delaunay Triangulation. (The filtration value is set to NaN, which stands for unknown value):
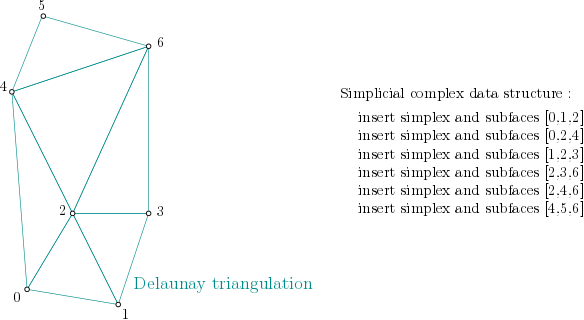
Simplex tree structure construction example¶
Filtration value computation algorithm¶
for i : dimension → 0 do
for all σ of dimension i
if filtration(σ) is NaN then
filtration(σ) = α²(σ)
end if
for all τ face of σ do // propagate alpha filtration value
if filtration(τ) is not NaN then
filtration(τ) = min( filtration(τ), filtration(σ) )
else
if τ is not Gabriel for σ then
filtration(τ) = filtration(σ)
end if
end if
end for
end for
end for
make_filtration_non_decreasing()
prune_above_filtration()
Dimension 2¶
From the example above, it means the algorithm looks into each triangle ([0,1,2], [0,2,4], [1,2,3], …), computes the filtration value of the triangle, and then propagates the filtration value as described here:
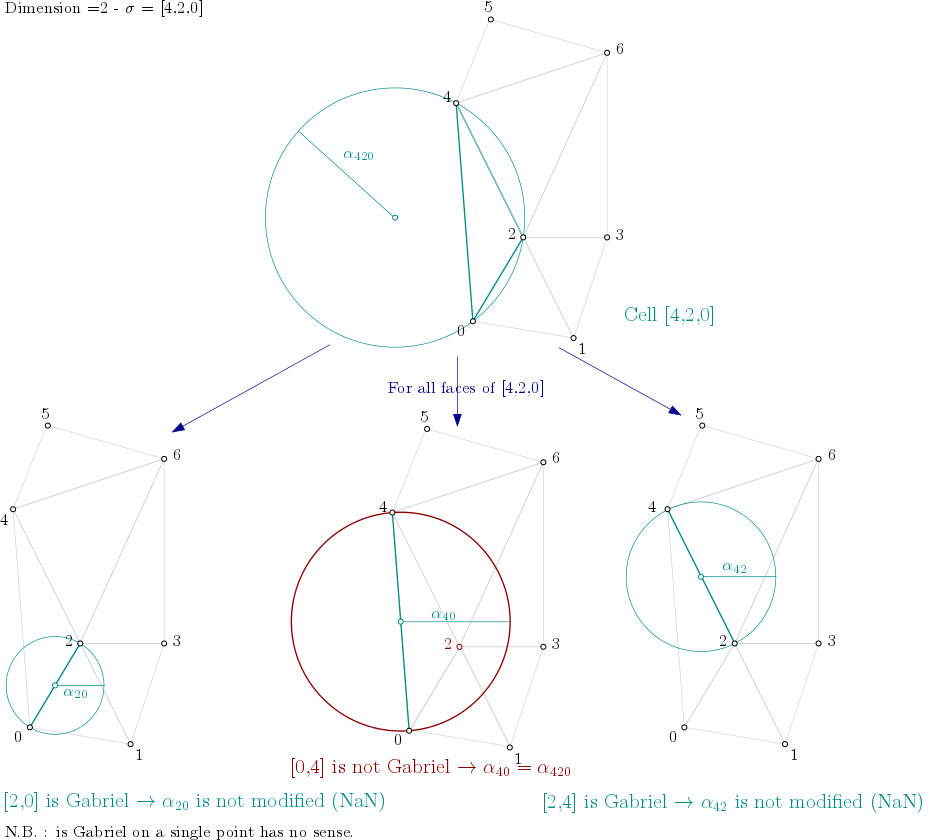
Filtration value propagation example¶
Dimension 1¶
Then, the algorithm looks into each edge ([0,1], [0,2], [1,2], …), computes the filtration value of the edge (in this case, propagation will have no effect).
Dimension 0¶
Finally, the algorithm looks into each vertex ([0], [1], [2], [3], [4], [5] and [6]) and sets the filtration value (0 in case of a vertex - propagation will have no effect).
Non decreasing filtration values¶
As the squared radii computed by CGAL are an approximation, it might happen that these
\(\alpha^2\) values do not quite define a proper filtration (i.e. non-decreasing with
respect to inclusion).
We fix that up by calling make_filtration_non_decreasing() (cf.
C++ version).
Prune above given filtration value¶
The simplex tree is pruned from the given maximum \(\alpha^2\) value (cf.
prune_above_filtration()). Note that this does not provide any kind
of speed-up, since we always first build the full filtered complex, so it is recommended not to use
max_alpha_square.
In the following example, a threshold of \(\alpha^2 = 32.0\) is used.
Example from OFF file¶
This example builds the Delaunay triangulation from the points given by an OFF file, and initializes the alpha complex with it.
Then, it is asked to display information about the alpha complex:
import gudhi
alpha_complex = gudhi.AlphaComplex(off_file=gudhi.__root_source_dir__ + \
'/data/points/alphacomplexdoc.off')
simplex_tree = alpha_complex.create_simplex_tree(max_alpha_square=32.0)
result_str = 'Alpha complex is of dimension ' + repr(simplex_tree.dimension()) + ' - ' + \
repr(simplex_tree.num_simplices()) + ' simplices - ' + \
repr(simplex_tree.num_vertices()) + ' vertices.'
print(result_str)
fmt = '%s -> %.2f'
for filtered_value in simplex_tree.get_filtration():
print(fmt % tuple(filtered_value))
the program output is:
Alpha complex is of dimension 2 - 20 simplices - 7 vertices.
[0] -> 0.00
[1] -> 0.00
[2] -> 0.00
[3] -> 0.00
[4] -> 0.00
[5] -> 0.00
[6] -> 0.00
[2, 3] -> 6.25
[4, 5] -> 7.25
[0, 2] -> 8.50
[0, 1] -> 9.25
[1, 3] -> 10.00
[1, 2] -> 11.25
[1, 2, 3] -> 12.50
[0, 1, 2] -> 13.00
[5, 6] -> 13.25
[2, 4] -> 20.00
[4, 6] -> 22.74
[4, 5, 6] -> 22.74
[3, 6] -> 30.25