
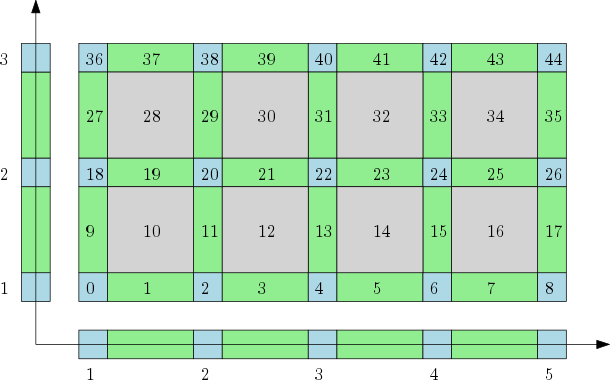
| The cubical complex is an example of a structured complex useful in computational mathematics (specially rigorous numerics) and image analysis. | Author: Pawel Dlotko Introduced in: GUDHI 1.3.0 Copyright: MIT |
| User manual: Cubical complex | ||

| The simplex tree is an efficient and flexible data structure for representing general (filtered) simplicial complexes. The data structure is described in [7] . | Author: Clément Maria Introduced in: GUDHI 1.0.0 Copyright: MIT |
| User manual: Filtered Complexes | ||
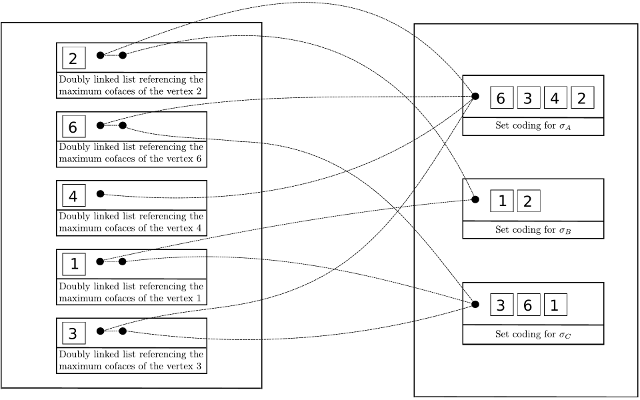
| The Toplex map data structure is composed firstly of a raw storage of toplices (the maximal simplices) and secondly of a map which associate any vertex to a set of pointers toward all toplices containing this vertex. | Author: François Godi Introduced in: GUDHI 2.1.0 Copyright: MIT |
| User manual: Toplex Map | ||

| The Skeleton-Blocker data-structure proposes a light encoding for simplicial complexes by storing only an implicit representation of its simplices [2],[3]. Intuitively, it just stores the 1-skeleton of a simplicial complex with a graph and the set of its "missing faces" that is very small in practice. This data-structure handles all simplicial complexes operations such as simplex enumeration or simplex removal but operations that are particularly efficient are operations that do not require simplex enumeration such as edge iteration, link computation or simplex contraction. | Author: David Salinas Introduced in: GUDHI 1.1.0 Copyright: MIT |
| User manual: Skeleton-Blocker | ||

| The purpose of this package is to offer a user-friendly interface for edge contraction simplification of huge simplicial complexes. It uses the Skeleton-Blocker data-structure whose size remains small during simplification of most used geometrical complexes of topological data analysis such as the Rips or the Delaunay complexes. In practice, the size of this data-structure is even much lower than the total number of simplices. | Author: David Salinas Introduced in: GUDHI 1.1.0 Copyright: MIT (LGPL v3) Requires: CGAL ≥ 4.11.0 |
| User manual: Edge contraction | ||
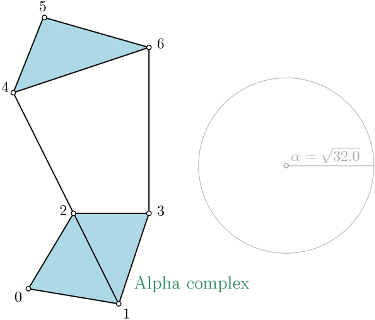
| Alpha complex is a simplicial complex constructed from the finite cells of a Delaunay Triangulation. The filtration value of each simplex is computed as the square of the circumradius of the simplex if the circumsphere is empty (the simplex is then said to be Gabriel), and as the minimum of the filtration values of the codimension 1 cofaces that make it not Gabriel otherwise. All simplices that have a filtration value \( > \alpha^2 \) are removed from the Delaunay complex when creating the simplicial complex if it is specified. For performances reasons, it is advised to use CGAL ≥ 5.0.0. | Author: Vincent Rouvreau Introduced in: GUDHI 1.3.0 Copyright: MIT (GPL v3) Requires: Eigen ≥ 3.1.0 and CGAL ≥ 4.11.0 |
| User manual: Alpha complex | ||
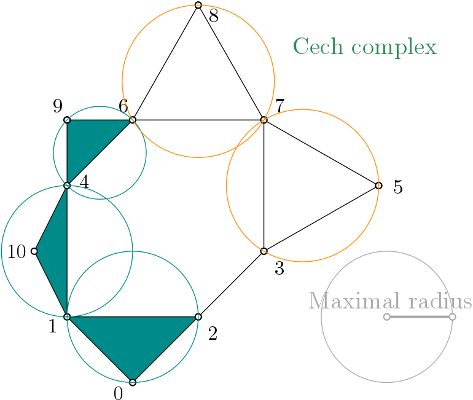
| The Čech complex is a simplicial complex constructed from a proximity graph. The set of all simplices is filtered by the radius of their minimal enclosing ball. | Author: Vincent Rouvreau, Hind Montassif Introduced in: GUDHI 2.2.0 Copyright: MIT (LGPL v3) Requires: CGAL |
| User manual: Čech complex | ||
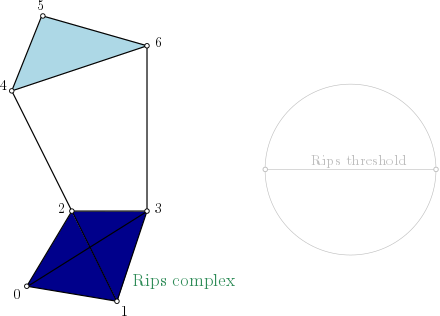
| Rips complex is a simplicial complex constructed from a one skeleton graph. The filtration value of each edge is computed from a user-given distance function and is inserted until a user-given threshold value. This complex can be built from a point cloud and a distance function, or from a distance matrix. | Author: Clément Maria, Pawel Dlotko, Vincent Rouvreau, Marc Glisse Introduced in: GUDHI 2.0.0 Copyright: MIT |
| User manual: Rips complex | ||

| Edge collapse is able to reduce any flag filtration to a smaller flag filtration with the same persistence, using only the 1-skeletons of a simplicial complex. The reduction is exact and the persistence homology of the reduced sequence is identical to the persistence homology of the input sequence. The resulting method is simple and extremely efficient. Computation of edge collapse and persistent homology of a filtered flag complex via edge collapse as described in [33]. | Author: Siddharth Pritam, Marc Glisse Introduced in: GUDHI 3.3.0 Copyright: MIT |
| User manual: Edge collapse | ||
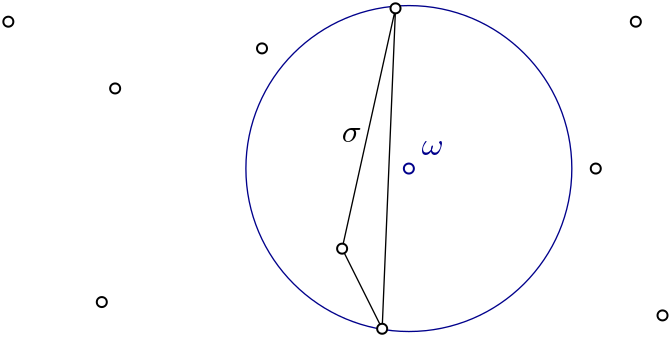
| Witness complex \( Wit(W,L) \) is a simplicial complex defined on two sets of points in \(\mathbb{R}^D\). The data structure is described in [7] . | Author: Siargey Kachanovich Introduced in: GUDHI 1.3.0 Copyright: MIT (GPL v3 for Euclidean version) Euclidean version requires: Eigen ≥ 3.1.0 and CGAL ≥ 4.11.0 |
| User manual: Witness complex | ||

| Nerves and Graph Induced Complexes are cover complexes, i.e. simplicial complexes that provably contain topological information about the input data. They can be computed with a cover of the data, that comes i.e. from the preimage of a family of intervals covering the image of a scalar-valued function defined on the data. | Author: Mathieu Carrière Introduced in: GUDHI 2.1.0 Copyright: MIT (GPL v3) Requires: CGAL ≥ 4.11.0 |
| User manual: Cover complex | ||

| Coxeter triangulation module is designed to provide tools for constructing a piecewise-linear approximation of an \(m\)-dimensional smooth manifold embedded in \( \mathbb{R}^d \) using an ambient triangulation. | Author: Siargey Kachanovich Introduced in: GUDHI 3.4.0 Copyright: MIT (LGPL v3) Requires: Eigen ≥ 3.1.0 |
| User manual: Coxeter triangulation | ||

| A Tangential Delaunay complex is a simplicial complex designed to reconstruct a \( k \)-dimensional manifold embedded in \( d \)-dimensional Euclidean space. The input is a point sample coming from an unknown manifold. The running time depends only linearly on the extrinsic dimension \( d \) and exponentially on the intrinsic dimension \( k \). | Author: Clément Jamin Introduced in: GUDHI 2.0.0 Copyright: MIT (GPL v3) Requires: Eigen ≥ 3.1.0 and CGAL ≥ 4.11.0 |
| User manual: Tangential complex | ||
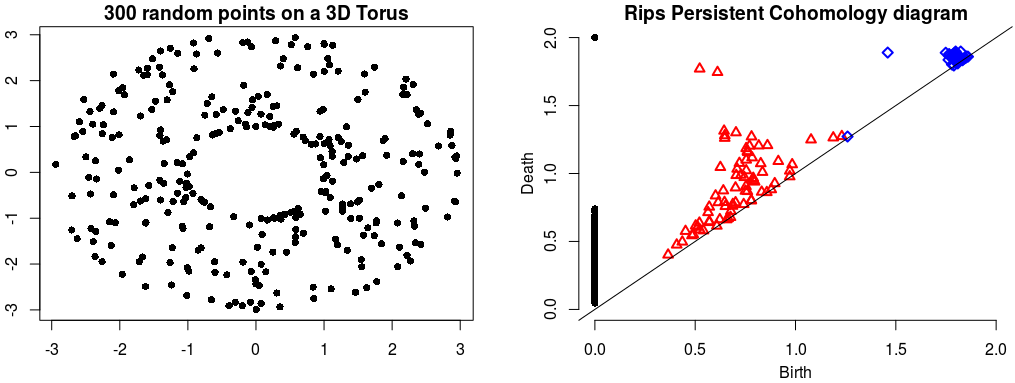
| The theory of homology consists in attaching to a topological space a sequence of (homology) groups, capturing global topological features like connected components, holes, cavities, etc. Persistent homology studies the evolution – birth, life and death – of these features when the topological space is changing. Consequently, the theory is essentially composed of three elements: topological spaces, their homology groups and an evolution scheme. Computation of persistent cohomology using the algorithm of [23] and [26] and the Compressed Annotation Matrix implementation of [8] . | Author: Clément Maria Introduced in: GUDHI 1.0.0 Copyright: MIT |
| User manual: Persistent Cohomology | ||
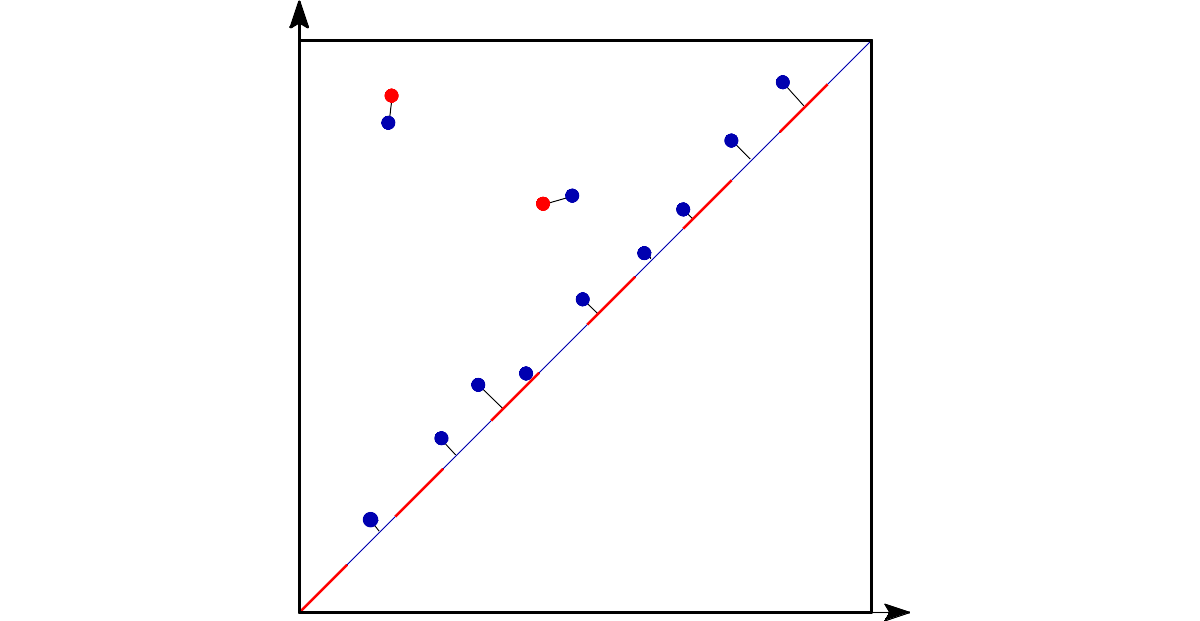
| Bottleneck distance measures the similarity between two persistence diagrams. It's the shortest distance b for which there exists a perfect matching between the points of the two diagrams (+ all the diagonal points) such that any couple of matched points are at distance at most b, where the distance between points is the sup norm in \(\mathbb{R}^2\) (not the Euclidean distance). | Author: François Godi Introduced in: GUDHI 2.0.0 Copyright: MIT (GPL v3) Requires: CGAL ≥ 4.11.0 |
| User manual: Bottleneck distance | ||
| It contains implementation of various representations of persistence diagrams; diagrams themselves, persistence landscapes (rigorous and grid version), persistence heat maps, vectors and others. It implements basic functionalities which are necessary to use persistence in statistics and machine learning. | Author: Pawel Dlotko Introduced in: GUDHI 2.1.0 Copyright: MIT |
| User manual: Persistence representations | ||
| \((x_1,\ldots,x_d)\) | This contains various tools to handle point clouds: spatial searching, subsampling, etc. | Author:Clément Jamin, Siargey Kachanovich, Marc Glisse Introduced in: GUDHI 1.3.0 Copyright: MIT (GPL v3) |
| Manuals: Spatial_searching, Subsampling | ||